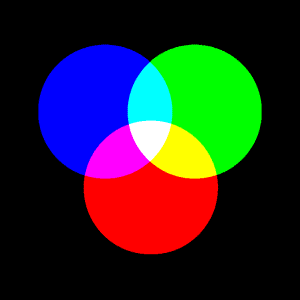
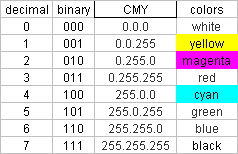
One would like to assume that the two systems represented were as different as day and night. However, it is more complicated, yet, the differantials don't necessarily have to be dissected or deciphered. Instead the rules on which the colors in the pictures, drawings and books on this site are based, shall be put on display. Hence the table above didn't show a K-fraction, which as black is a stable component of CMYK, within the subtractive color system. In this kind of painting and the drawings respectively, both done in Indian ink, black only exists as the result of the concurrence or interaction of the three base colors.
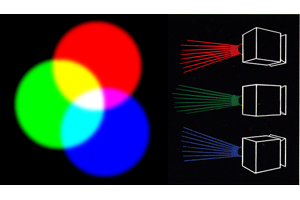
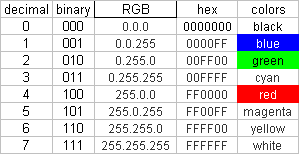
The binary system is perfectly suited to demonstrate the systems. It proofed obviously in this scale. The three base colors RGB or CMYK and the three digits of the binary number are decisive for everything that follows. Through the 3 digits there can be depicted the first 8 numbers from 0 to 7, as the starting scale of 8 colors evolves from the 3 base colors – or even more precisely 7 colors and the base (color) 0. In a projection of light the latter = Black/ no light, with drawing and painting normally= White (the background).
Since the application of this principle in painting and drawing is not about exact mathematics, but entirely about colors, there is no reason for forcefully retaining a particular color attribution, it can be exchanged in any order. In this way, the mathematical system is applied for control only. Through this different attribution 6 varied compositions (or color directions) are possible, the first one was depicted above, here are all of them once more:
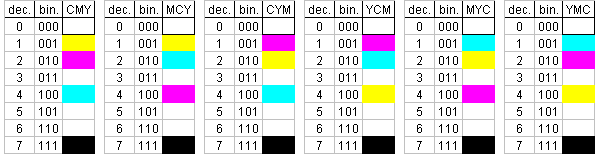
So far the base color-scale of 8 colors = 3 binary digits.
The hue increases according to the further binary digits, e.g. with 6 digits there are 64 colors. Correspondingly, the 3 base colors now have to be shaded and dispersed among 6 digits. Therefore, they have to keep the proportion 1:2 respectively, in order to make the addition result in a full tone. In this case, one binary digit at a time stands for 1/3 cyan and 2/3 cyan, one at a time for 1/3 and 2/3 magenta and one for 1/3 and 2/3 yellow. The order in which they are allocated is free again and thus 6 binary digits already produce 720 possibilities or permutations.
Here the starting basis, in 2 degrees CMY respectively:
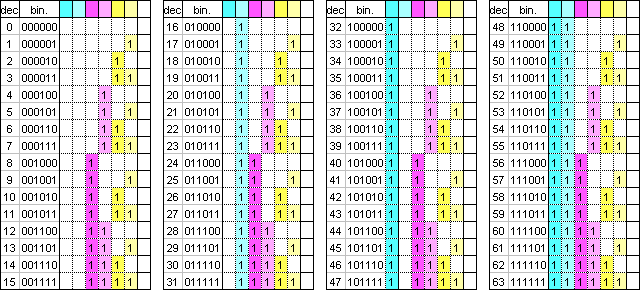
and the scale resulting from it:

In the main features the way colors are handled here, should be somewhat more intelligible now. Not all details can or should be discussed, by other means the separate works of art will possibly be capable of it, step by step.